交叉验证

怎么评估模型的好坏？把获取的全部训练数据分成两份：一份用于测试，一份用于训练。然后用前者来评估模型。

把全部训练数据分为测试数据和训练数据的做法称为交叉验证（Cross-validation）。

交叉验证的方法中，尤为有名的是 K 折交叉验证（k-fold cross-validation）：

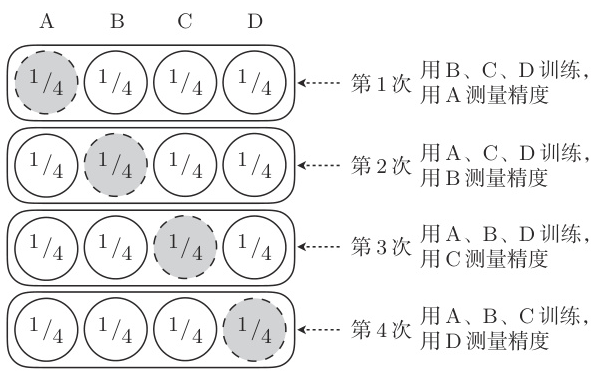
回归

对于回归的情况，只要在训练好的模型上计算测试数据的误差的平方，再取其平均值就可以了，这个值称为均方误差（MSE, Mean Square Error）：

MSE=1n∑i=1n(y(i)−fθ(x(i)))2MSE = \frac{1}{n}\sum_{i=1}^{n}(y^{(i)} - f_{\bm\theta}(\bm x^{(i)}))^2

分类

我们需要考虑到答案是否正确，关于分类的结果，就会有以下的四种情况：

混淆矩阵(Confusion Matrix) 是一种在机器学习和统计学中用于评估分类模型性能的工具，它以表格形式展示了模型预测结果与实际类别之间的关系。简单来说，混淆矩阵帮助我们了解模型在各个类别上的预测准确性和错误类型。

精度（Accuracy）是正确预测的比例：

Accuracy=TP+TNTP+FP+FN+TNAccuracy = \frac{TP + TN}{TP + FP + FN + TN}

用测试数据来计算这个值，值越高精度越高，也就意味着模型越好。

考虑一个场景，绝大多数数据都是正类（Positive），如果模型总是预测为正类，那么精度会很高，但实际上模型并没有学到任何有用的东西。
因此，精度并不能完全反映模型的好坏。

精确率和召回率

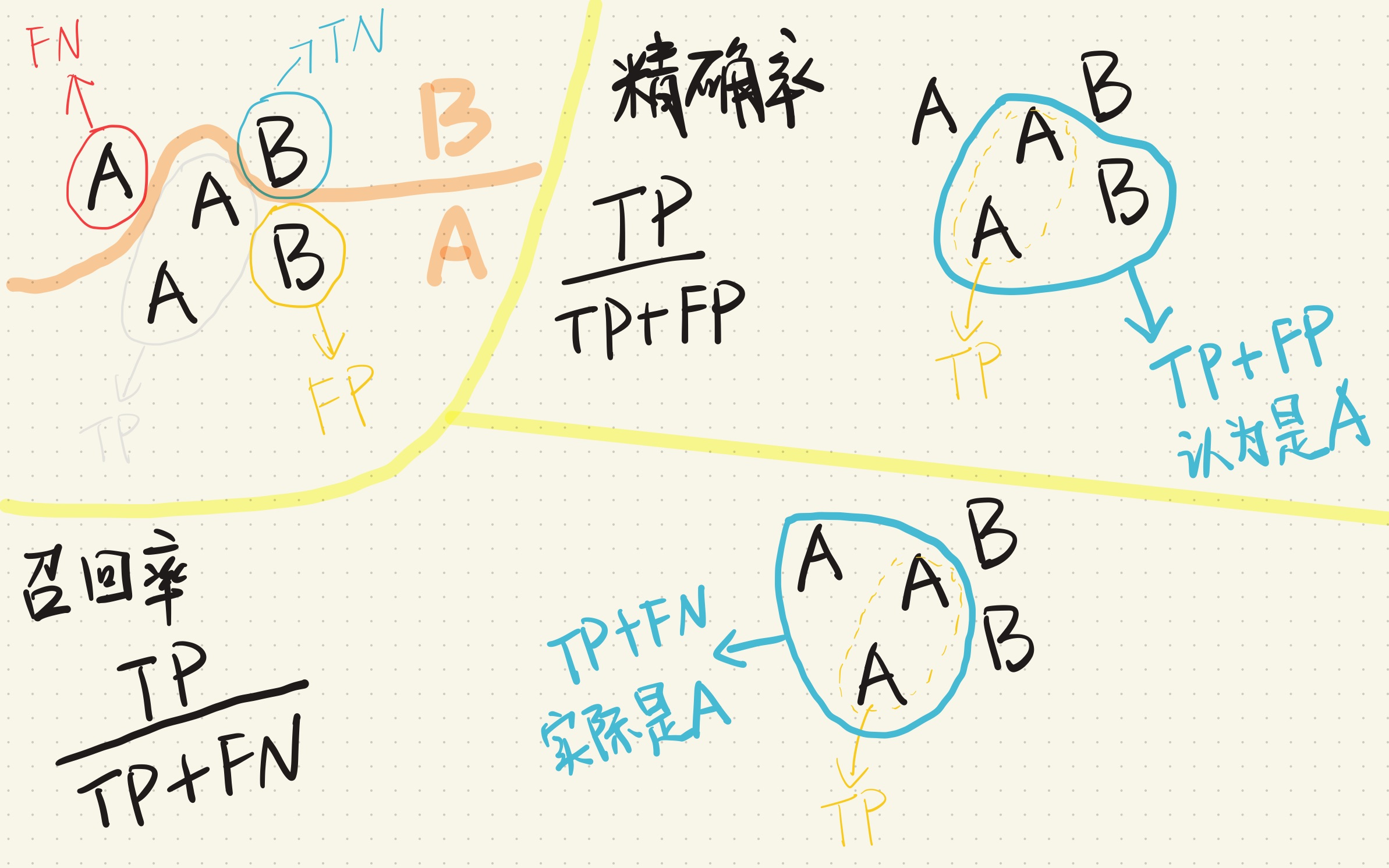
先来看精确率（Precision）：

Precision=TPTP+FPPrecision = \frac{TP}{TP + FP}

精确率衡量的是模型预测为正类的样本中，实际为正类的比例。

你说的黑，是不是真的黑？

高精确率意味着模型在预测正类时较少出现误报。

另一个指标是召回率（Recall）：

Recall=TPTP+FNRecall = \frac{TP}{TP + FN}

召回率衡量的是实际为正类的样本中，模型预测为正类的比例。

这么多的黑，你能找到多少？

高召回率意味着模型能够捕捉到大部分正类样本。

F-score

通常来说，精确率和召回率是一个平衡的关系。提高精确率可能会降低召回率，反之亦然。
为了综合考虑这两个指标，我们可以使用 F1 值（F1-measure），通常叫 F1 值，调和平均值：

F1measure=21Precision+1Recall=2⋅Precision⋅RecallPrecision+RecallF1_{measure} = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall}

还有一个更通用的加权 F 值：

Fweighted=(1+β2)⋅Precision⋅Recallβ2⋅Precision+RecallF_{weighted} = \frac{(1 + \beta^2) \cdot Precision \cdot Recall}{\beta^2 \cdot Precision + Recall}

注意到： F1measure=Fweighted  ⟺  β=1F1_{measure} = F_{weighted} \iff \beta = 1

过拟合

模型只能拟合训练数据的状态被称为过拟合（overfitting）。

有几种方法可以避免过拟合：

  • 增加全部训练数据的数量
  • 使用简单的模型：让模型没法高度拟合训练数据
  • 引入对参数的惩罚：正则化

正则化

正则化的目标是让模型的参数尽可能小，通常是通过在目标函数中添加一个惩罚项来实现。

回归的正则化

对于线性回归，目标函数可以写成：

E(θ)=12∑i=1n(y(i)−fθ(x(i)))2E(\bm\theta) = \frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-f_{\bm\theta}(\bm x^{(i)}))^2

给它添加一个惩罚项后：

E(θ)=12∑i=1n(y(i)−fθ(x(i)))2+λ2R(θ)R(θ)=∑j=1mθj2E(\bm\theta) = \frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-f_{\bm\theta}(\bm x^{(i)}))^2 + \frac{\lambda}{2} R(\bm\theta) \\ R(\bm\theta) = \sum_{j=1}^{m}\theta_j^2

  1. λ\lambda 是正则化系数，控制惩罚的强度。
  2. 因为一般不对偏置项 θ0\theta_0 进行正则化，所以从 j=1j=1 开始。

它可以防止参数变得过大，有助于参数接近较小的值。参数的值变小，意味着该参数的影响也会相应地变小。这是一种通过减小不需要的参数的影响，将复杂模型替换为简单模型来防止过拟合的方式。

分类的正则化

对于分类问题，目标函数可以添加正则化项后：

log⁡L(θ)=−∑i=1n(y(i)log⁡(fθ(x(i)))+(1−y(i))log⁡(1−fθ(x(i))))+λ2R(θ)R(θ)=∑j=1mθj2\log L(\bm\theta) = -\sum_{i=1}^{n} \left( y^{(i)}\log(f_{\bm\theta}(\bm x^{(i)})) + (1-y^{(i)})\log(1-f_{\bm\theta}(\bm x^{(i)})) \right) +\frac{\lambda}{2} R(\bm\theta) \\ R(\bm\theta) = \sum_{j=1}^{m}\theta_j^2

目标函数反转符号是为了将最大化问题替换为最小化问题

正则化后的微分

我们把目标函数 E(θ)E(\bm\theta) 拆成原来的目标函数 C(θ)C(\bm\theta) 和正则化项 R(θ)R(\bm\theta)：

E(θ)=C(θ)+R(θ)E(\bm\theta) = C(\bm\theta) + R(\bm\theta)

微分后：

∂E(θ)∂θj=∂C(θ)∂θj+∂R(θ)∂θj\frac{\partial E(\bm\theta)}{\partial \theta_j} = \frac{\partial C(\bm\theta)}{\partial \theta_j} + \frac{\partial R(\bm\theta)}{\partial \theta_j}

其中，正则化项的微分是：

∂R(θ)∂θj=λθj\frac{\partial R(\bm\theta)}{\partial \theta_j} = \lambda\theta_j

因此，正则化后的微分可以写成：

∂E(θ)∂θj=∂C(θ)∂θj+λθj\frac{\partial E(\bm\theta)}{\partial \theta_j} = \frac{\partial C(\bm\theta)}{\partial \theta_j} + \lambda\theta_j

注意到，因为 θ0\theta_0 不参与正则化，所以 ∂R(θ)∂θ0=0\frac{\partial R(\bm\theta)}{\partial \theta_0} = 0。
在更新参数的时候要对 j=0j = 0 的情况分情况讨论。

更新参数的公式就不写了，把正则化的部分加到对应的回归、逻辑回归的更新公式中即可。

L1正则化：R(θ)=∑j=1m∣θj∣L2正则化：R(θ)=∑j=1mθj2L1 正则化：R(\bm\theta) = \sum_{j=1}^{m}|\theta_j| \\ L2 正则化：R(\bm\theta) = \sum_{j=1}^{m}\theta_j^2

L1 正则化的特征是被判定为不需要的参数会变为 0，从而减少变
量个数。而 L2 正则化不会把参数变为 0。

欠拟合

欠拟合（underfitting）是指模型无法捕捉到数据中的重要模式或趋势，导致模型的预测性能较差。通常发生在模型过于简单，无法适应数据的复杂性时。

只根据精度不能判断是哪种不好的拟合。可以通过绘制学习曲线来判断：

欠拟合的情况是训练集和验证集的精度都很低，且两者相差不大：

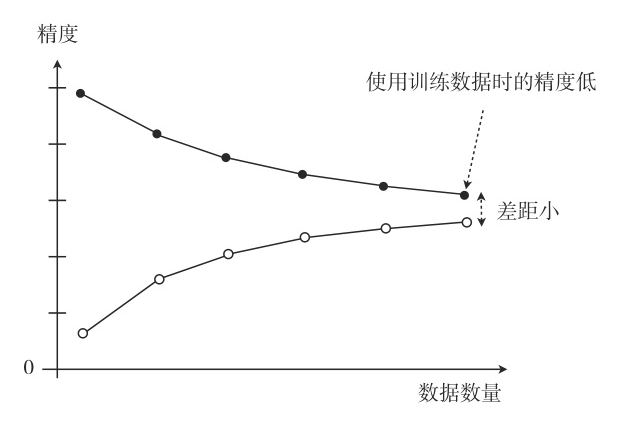
过拟合的情况是训练集的精度很高，而验证集的精度很低：

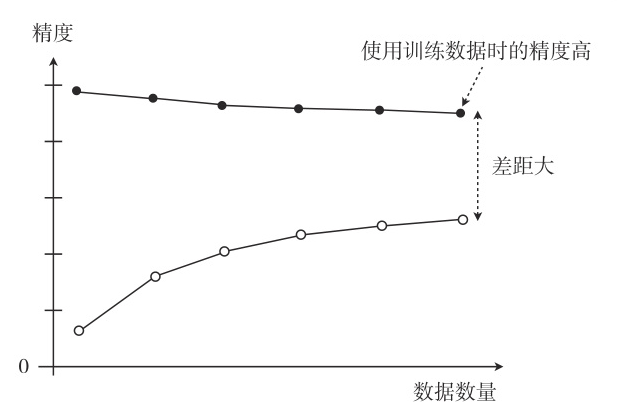
像这样展示了数据数量和精度的图称为学习曲线。