内积

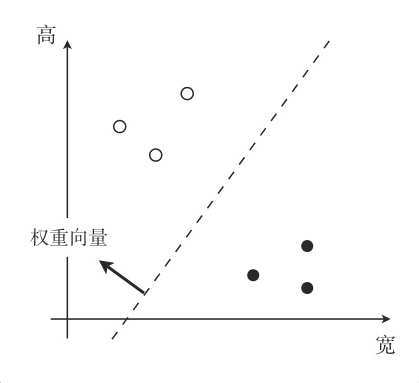
分类需要寻找一条以权重向量为法向量的直线，设法向量为 ww，那么直线的表达式可以通过向量的内积表示为：

实向量空间的内积是各相应元素乘积的和。

w⋅x=∑i=1nwixi=0\bm{w}\cdot\bm{x} = \sum_{i=1}^{n}w_{i}x_{i}=0

内积的另一种写法：

w⋅x=∣w∣⋅∣x∣⋅cosθ\bm{w}\cdot\bm{x} = |\bm{w}| \cdot |\bm{x}|\cdot cos\theta

要使内积为0，意味着 θ=90∘\theta=90^\circ 或者 θ=270∘\theta=270^\circ。

感知机

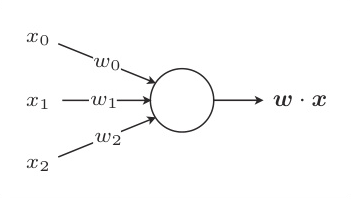
感知机是接受多个输入后将每个值与各自的权重相乘，最后输出总和的模型。

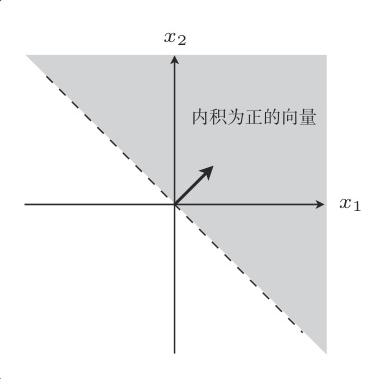
内积是衡量向量之间相似程度的指标。结果为正，说明二者相似；为 0 则二者垂直；为负则说明二者不相似。

分类的判别函数：
假设两个分类的标签（值）为 1 和 -1，

fw(x)={1(w⋅x≥0)−1(w⋅x<0)f_{\bm{w}}(\bm{x})= \begin{cases} 1 && (\bm{w} \cdot \bm{x} \ge 0) \\ -1 && (\bm{w} \cdot \bm{x} \lt 0) \end{cases}

更新权重的表达式可以写为

w:={w+y(i)x(i)(fw(x(i))≠y(i))w(fw(x(i))=y(i))\bm{w} := \begin{cases} \bm{w}+ y^{(i)}\bm{x}^{(i)} & & \left(f_{\bm{w}}(\bm{x}^{(i)})\ne y^{(i)}\right) \\ \bm{w} & & \left(f_{\bm{w}}(\bm{x}^{(i)}) = y^{(i)}\right) \end{cases}

这说明更新表达式只有在判别函数分类失败的时候才会更新参数值。

虽然有加法和减法的区别，但它们的做法都是在分类失败时更新权重向量，使得直线旋转相应的角度。像这样重复更新所有的参数，就是感知机的学习方法。

线性可分

感知机的缺点是它只能解决线性可分的问题，像这样不能用直线分类的就不是线性可分：

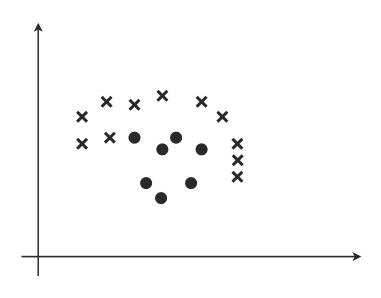
既然有单层，就会有多层，实际上多层感知机就是神经网络了。

逻辑回归

与回归的时候类似，我们也定义一个 fθ(x)f_{\bm \theta}(\bm x)：

fθ(x)=11+exp⁡(−θ⊤x)f_{\bm \theta}(\bm x) = \frac{1}{1 + \exp(-\bm\theta^\top\bm x)}

这个叫做 sigmoid 函数。

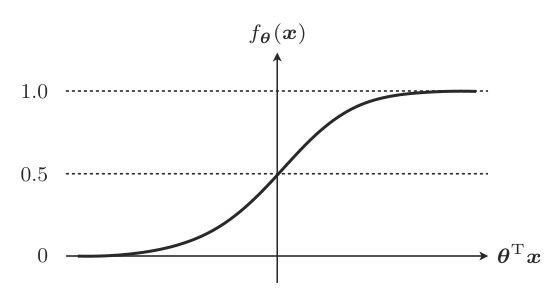
几个重要的特性：

  1. θ⊤x=0\bm\theta^\top\bm x = 0 时，fθ(x)=0.5f_{\bm \theta}(\bm x) = 0.5
  2. 0<fθ(x)<10 \lt f_{\bm \theta}(\bm x) \lt 1

    因为这个取值范围，所以它可以作为概率来使用。

把函数的输出解释为“在给出数据 x\bm{x} 时候，样本属于类别 1”的条件概率，即：

fθ(x)=P(y=1∣x)f_{\bm \theta}(\bm x) = P(y=1 \mid \bm x)

根据 sigmod 的性质，有：

y={1(fθ(x)≥0.5)0(fθ(x)<0.5)  ⟹  y={1(θ⊤x≥0)0(θ⊤x<0)y= \begin{cases} 1 & & ({f_{\bm \theta}(\bm x) \ge 0.5}) \\ 0 & & ({f_{\bm \theta}(\bm x) \lt 0.5}) \end{cases} \implies y= \begin{cases} 1 & & ({\bm\theta^\top\bm x \ge 0}) \\ 0 & & ({\bm\theta^\top\bm x \lt 0}) \end{cases}

我们称直线 θ⊤x=0{\bm\theta^\top\bm x = 0} 就是决策边界。
为了求得正确的参数 θ\bm\theta 而定义目标函数，进行微分，然后求参数的更新表达式，这种算法就叫逻辑回归。

似然函数

假定所有的训练数据都是互不影响、独立发生的，这种情况下整体的概率就可以用下面的联合概率来表示：

L(θ)=∏i=1nP(y(i)=1∣x(i))y(i)P(y(i)=0∣x(i))1−y(i)L(\bm\theta) = \prod_{i=1}^{n} P(y^{(i)}=1\mid\bm x^{(i)})^{y^{(i)}} P(y^{(i)}=0\mid\bm x^{(i)})^{1-y^{(i)}}

这个函数叫做似然函数（Likelihood）。

这个表达式利用了任何数字的 0 次方都是 1 的特性，其实乘起来有一个 P(y∣x)P(y\mid x) 是 0。

现在考虑的是联合概率，我们希望概率尽可能大，所以要最大化。我们可以认为似然函数 L(θ)L(\bm\theta) 中，使其值最大的参数 θ\theta 能够最近似地说明训练数据。

对数似然函数

直接对似然函数进行微分有点困难，在此之前要把函数变形一下，取对数就可以了：

log⁡L(θ)=log⁡∏i=1nP(y(i)=1∣x(i))y(i)P(y(i)=0∣x(i))1−y(i)=∑i=1n(log⁡P(y(i)=1∣x(i))y(i)+log⁡P(y(i)=0∣x(i))1−y(i))  ⟸  log⁡(ab)=log⁡a+log⁡b=∑i=1n(y(i)log⁡P(y(i)=1∣x(i))+(1−y(i))log⁡P(y(i)=0∣x(i)))  ⟸  log⁡(ab)=blog⁡a=∑i=1n(y(i)log⁡P(y(i)=1∣x(i))+(1−y(i))log⁡(1−P(y(i)=1∣x(i))))  ⟸  P(y(i)=0∣x(i))=1−P(y(i)=1∣x(i))=∑i=1n(y(i)log⁡fθ(x(i))+(1−y(i))log⁡(1−fθ(x(i))))  ⟸  P(y=1∣x)=fθ(x)\begin{aligned} \log L(\bm\theta) &= \log \prod_{i=1}^{n} P(y^{(i)}=1\mid\bm x^{(i)})^{y^{(i)}} P(y^{(i)}=0\mid\bm x^{(i)})^{1-y^{(i)}} \\ &=\sum_{i=1}^{n} \left( \log P(y^{(i)}=1\mid\bm x^{(i)})^{y^{(i)}} + \log P(y^{(i)}=0\mid\bm x^{(i)})^{1-y^{(i)}} \right) && \impliedby \log(ab)=\log a + \log b \\ &=\sum_{i=1}^{n} \left( {y^{(i)}} \log P(y^{(i)}=1\mid\bm x^{(i)}) + ({1-y^{(i)}}) \log P(y^{(i)}=0\mid\bm x^{(i)}) \right) && \impliedby \log(a^b)=b \log a \\ &=\sum_{i=1}^{n} \left( {y^{(i)}} \log P(y^{(i)}=1\mid\bm x^{(i)}) + ({1-y^{(i)}}) \log (1 - P(y^{(i)}=1\mid\bm x^{(i)})) \right) && \impliedby P(y^{(i)}=0\mid\bm x^{(i)}) = 1 - P(y^{(i)}=1\mid\bm x^{(i)}) \\ &=\sum_{i=1}^{n} \left( {y^{(i)}} \log f_{\bm\theta}(\bm x^{(i)}) + ({1-y^{(i)}}) \log (1 - f_{\bm\theta}(\bm x^{(i)})) \right) && \impliedby P(y=1 \mid \bm x) = f_{\bm \theta}(\bm x) \end{aligned}

然后要对似然函数做微分：

log⁡L(θ)=∑i=1n(y(i)log⁡fθ(x(i))+(1−y(i))log⁡(1−fθ(x(i))))\log L(\bm\theta) = \sum_{i=1}^{n} \left( {y^{(i)}} \log f_{\bm\theta}(\bm x^{(i)}) + ({1-y^{(i)}}) \log (1 - f_{\bm\theta}(\bm x^{(i)})) \right)

∂∂θjlog⁡L(θ)=∂∂θj∑i=1n(y(i)log⁡fθ(x(i))+(1−y(i))log⁡(1−fθ(x(i))))\frac{\partial}{\partial\theta_j} \log L(\bm\theta) = \frac{\partial}{\partial\theta_j} \sum_{i=1}^{n} \left( {y^{(i)}} \log f_{\bm\theta}(\bm x^{(i)}) + ({1-y^{(i)}}) \log (1 - f_{\bm\theta}(\bm x^{(i)})) \right)

使用复合函数：

u=log⁡L(θ)v=fθ(x)=11+exp⁡(−θ⊤x)\begin{aligned} u &= \log L(\bm\theta) \\ v &= f_{\bm\theta}(\bm x) = \frac{1}{1 + \exp(-\bm\theta^\top\bm x)} \end{aligned}

链式法则启动：

∂u∂θj=∂u∂v⋅∂v∂θj\frac{\partial u}{\partial \theta_j} = \frac{\partial u}{\partial v} \cdot \frac{\partial v}{\partial \theta_j}

第一部分：

∂u∂v=∂log⁡L(θ)∂fθ(x)=∂∂v∑i=1n(y(i)log⁡v+(1−y(i))log⁡(1−v))  ⟸  代入fθ(x)=v=∑i=1n(y(i)v−1−y(i)1−v)  ⟸  log⁡(x)=1x,注意−v中的负号\begin{aligned} \frac{\partial u}{\partial v} &=\frac{\partial \log L(\bm\theta)}{\partial f_{\bm\theta}(\bm x)} \\ &=\frac{\partial}{\partial v} \sum_{i=1}^{n} \left( {y^{(i)}} \log v + ({1-y^{(i)}}) \log (1 - v) \right) && \impliedby 代入 f_{\bm\theta}(\bm x) = v \\ &= \sum_{i=1}^{n}\left(\frac{y^{(i)}}{v} - \frac{1-y^{(i)}}{1-v} \right) && \impliedby \log (x) = \frac{1}{x}, 注意 -v 中的负号 \end{aligned}

第二部分：

插播 sigmod 函数的导数： dσ(x)dx=σ(x)(1−σ(x))\frac{d\sigma(x)}{dx} = \sigma(x)(1-\sigma(x))

∂v∂θj=v(1−v)∂∂θjθ⊤x  ⟸  θ⊤x看成一个元=v(1−v)xj\begin{aligned} \frac{\partial v}{\partial \theta_j} &= v(1-v) \frac{\partial}{\partial \theta_j} \bm\theta^\top \bm x && \impliedby {\bm\theta^\top \bm x} \text{看成一个元} \\ &= v(1-v) x_j \end{aligned}

结合一下：

∂u∂θj=∑i=1n(y(i)v−1−y(i)1−v)⋅v(1−v)xj(i)=∑i=1n(y(i)−v)xj(i)=∑i=1n(y(i)−fθ(x(i)))xj(i)\begin{aligned} \frac{\partial u}{\partial \theta_j} &= \sum_{i=1}^{n} \left(\frac{y^{(i)}}{v} - \frac{1-y^{(i)}}{1-v} \right)\cdot v(1-v) x_j^{(i)} \\ &= \sum_{i=1}^{n} \left(y^{(i)}-v \right)x_j^{(i)} \\ &= \sum_{i=1}^{n} \left(y^{(i)}-f_{\bm\theta}(\bm x^{(i)}) \right)x_j^{(i)} \end{aligned}

因为我们需要最大化似然函数的值，所以参数要与微分结果同方向移动，所以更新参数的表达式为，：

θj:=θj+η∑i=1n(y(i)−fθ(x(i)))xj(i)\bm\theta_j := \bm\theta_j + \eta\sum_{i=1}^{n} \left(y^{(i)} - f_{\bm\theta}(\bm x^{(i)}) \right)x_j^{(i)}

可以取个反，这样就跟回归的时候一样了：

θj:=θj−η∑i=1n(fθ(x(i)−y(i)))xj(i)\bm\theta_j := \bm\theta_j - \eta\sum_{i=1}^{n} \left(f_{\bm\theta}(\bm x^{(i)} - y^{(i)}) \right)x_j^{(i)}