最小二乘法
假设有二元函数:
fθ(x)=θ0+θ1x
我们将训练数据中的广告费代入 fθ(x) ,把得到的点击量与训练数据中的点击量相比较,然后找出使二者的差最小的 θ,这种问题叫做最优化问题。
误差之和可以用表达式表示,称为目标函数:
E(θ)=21i=1∑n(y(i)−fθ(x(i)))2
- 这里的 x(i) 是指第 i 个训练数据,不是次幂。
- 为了避免误差相互抵消,所以不能简单把误差累加;这里不用绝对值用平方,是因为后面要微分,平方的微分比绝对值简单。
最速下降法
微分是计算变化的快慢程度时使用的方法。
对于一个函数 f(x) 来说,只要向与导数的符号相反的方向移动 x,f(x) 就会自然而然地沿着极小值的方向前进了。
这也被称为最速下降法(Steepest descent) 或 梯度下降(Gradient descent) 法:
x:=x−ηdxdf(x)
η 是称为学习率的正常数,影响收敛速度,甚至可能导致计算结果无法收敛。
fθ(x) 是关于 θ0,θ1 的双变量函数,所以不能用普通的微分 dxd,要用偏微分:
θ0:=θ0−η∂θ0∂E
θ1:=θ1−η∂θ1∂E
发现 u(θ) 不是对 θ 的直接函数,可以考虑使用复合函数的微分法则,假设:
u=E(θ)v=fθ(x)
则有:
∂θi∂u=∂v∂u⋅∂θi∂v
先求第一部分的导数:
∂v∂u=∂v∂(21i=1∑n(y(i)−v)2)=21i=1∑n(∂v∂u(y(i)−v)2)=21i=1∑n(∂v∂u(y(i)2−2y(i)v+v2))=21i=1∑n(−2y(i)+2v)=i=1∑n(v−y(i))⟸代入Eθ⟸微分分配律⟸展开平方⟸对v求导⟸常量提取
然后是第二部分:
∂θ0∂v=∂θ0∂(θ0+θ1x)=1∂θ1∂v=∂θ1∂(θ0+θ1x)=x
多项式回归
增加函数中多项式的次数,然后再使用函数的分析方法被称为多项式回归:
fθ(x)=θ0+θ1x+θ2x2+⋯+θnxn
偏导数对应更新就好了:
θn:=θn−η∂θn∂u
多重回归
与多项式回归增加变量的幂次数不同,多重回归描述的是包含多个变量的回归场景。
fθ(x1,…,xn)=θ0+θ1x1+⋯+θnxn
然后使用列向量来表示:
θ=⎣⎢⎢⎢⎢⎢⎢⎡θ0θ1θ2⋮θn⎦⎥⎥⎥⎥⎥⎥⎤,x=⎣⎢⎢⎢⎢⎢⎢⎡x0x1x2⋮xn⎦⎥⎥⎥⎥⎥⎥⎤(x0=1)
那么:
fθ(x)=θ⊤x
算偏导数也是一样的,用链式法则,只需要重新算一下第二部分:
∂θj∂vθj=∂θj∂(θ⊤x)=∂θj∂(θ0x0+θ1x1+⋅⋅⋅+θnxn)=xj:=θj−ηi=1∑n(fθ(x(i))−y(i))xj(i)
随机梯度下降法
用最速下降法来找函数的最小值时,选用随机数作为初始值的情况比较多。不过这样每次初始值都会变,进而导致陷入局部最优解的问题。
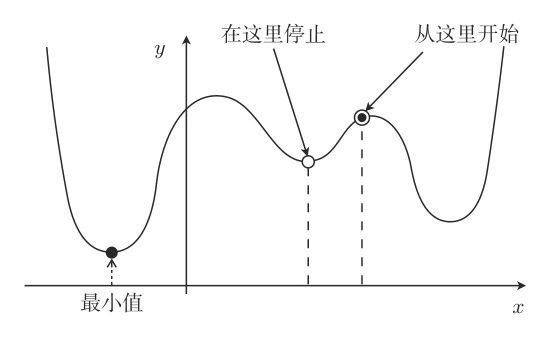
而在随机梯度下降法中会随机选择 m 个训练数据,并使用它来更新参数:
θj:=θj−ηk∈K∑(fθ(x(k))−y(k))xj(k)
这种做法被称为 小批量(mini-batch) 梯度下降法。

